Funções de Distribuição das Interrupções

Por que é importante conhecermos a distribuição de DEC, FEC, CHI¹ das interrupções?

Introdução

Não é raro fazermos analogias e interpretações baseadas em métricas como a média, mas é importante lembrar que seu uso pode levar a grandes equívocos de interpretação.

Embora a média seja frequentemente uma métrica útil, ela pode ser enganosa quando há uma quantidade significativa de valores muito baixos ou muito altos que distorcem o resultado. Isso é particularmente relevante ao analisar dados de interrupções, o que será discutido neste artigo através de algumas funções de distribuição que melhor representam essa distribuição.

Importância do entendimento das métricas

Na Figura 1 é ilustrado um exemplo real de distribuição do CHI Total de um conjunto elétrico ao longo do ano.

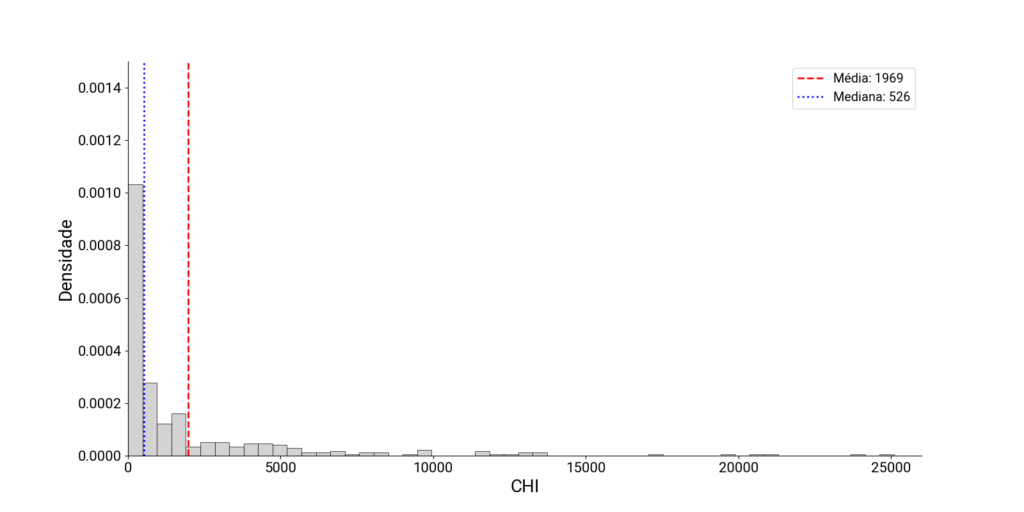
Para a maioria dos casos na natureza, a distribuição normal é bem aceita, onde a média coincide com a mediana e a moda. No entanto, há uma diferença significativa entre essas métricas:

• Média: é a soma de todos os valores dividido pela quantidade.
• Mediana: é a métrica que indica onde fica metade da quantidade dos valores.
• Moda: é o valor que mais ocorre

Na Figura 1, nota-se como a média é sensível a baixas frequências, mas a grandes valores de CHI, deslocando-se na direção de CHIs elevados. Nesse caso, a média ultrapassa o dobro da mediana. Por exemplo, a influência de um dia com cerca de 25.000 CHI equivale a 50 dias de 500 CHI (valor aproximado da mediana).

Focando na melhoria dos processos

Quando buscamos melhorias para mitigar o DEC e FEC, devemos considerar que interrupções de grande magnitude são raras, mas podem comprometer os indicadores. Interrupções raras geralmente decorrem de eventos incomuns, como a falta de peças ou dificuldades de acesso. Por serem infrequentes, esses eventos muitas vezes não têm procedimentos predefinidos e o processo de aprendizagem ocorre durante a solução do problema.

Por outro lado, interrupções com baixo CHI mas elevada frequência muitas vezes passam despercebidas. A análise mais simples é a comparação, considerando fatores como histórico e características semelhantes. Um exemplo é o DC – Dia Crítico², definido como a média acrescida de três desvios padrões dos valores diários.

Focar apenas nos dias de elevado CHI é improdutivo. O ideal é olhar para pequenos ganhos no CHI com alta frequência. Algumas vantagens de utilizar a mediana como métrica base são:

• A mediana reflete 50% dos casos, ao contrário da média que pode ser distorcida por grandes CHIs.
• A mediana não é sensível a grandes valores, enquanto a média é fortemente impactada.

Qual a melhor função de distribuição para curva de CHIs diários?

Entender a distribuição do CHI diário permite comparar a evolução ao longo dos anos e entre conjuntos elétricos. Se conjuntos possuem características similares, é natural assumir que tenham performances semelhantes. Além disso, traz informações importantes como saber se o dia está entre os 20% melhores ou piores. Conhecer a função de distribuição é crucial para estimar e/ou acompanhar a evolução do DEC ao final de um período.

Metodologia

O processo é muito semelhante do que foi feito no que foi apresentado no Dia de Rescaldo com a diferença de que lá foram considerados como expurgos somente ISE – Interrupção em situação de emergência e DC.

Baseando-se nos arquivos de interrupção disponíveis no site da ANEEL, verificam-se quais funções de distribuição melhor representam o CHI Total (Líquido + Expurgado) de cada conjunto elétrico a cada ano. Dias sem CHI são considerados com CHI zero, e outliers são retirados usando a formulação de Tukey³.

Foram avaliadas até 16 funções de distribuição diferentes, ranqueadas pela métrica AICc⁴.

Resultados

As quatro primeiras funções de distribuição dominaram as demais. A Tabela 1 mostra os resultados, com a Weibull Mixture obtendo o menor AICc 8861 vezes.

Tabela 1 – Mapa de calor do ranking das funções de distribuição

rank	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Distribution
Weibull_Mixture	8861	3865	2789	2258	627	469	405	360	585	132	89	72	98	12	32	3
Weibull_CR	5993	5419	2763	3069	817	653	865	480	240	147	82	51	70	19	6
Gamma_3P	4819	4766	5450	2390	720	760	737	499	177	344	11	2	1
Weibull_3P	611	4581	5720	6449	2000	620	420	231	27	12	3	2
Gamma_2P	13	96	622	2044	6370	3025	2927	898	1293	1073	2159	134	25
Weibull_2P	50	205	442	942	5339	8286	2104	2007	997	144	122	41
Weibull_DS		1	21	82	312	2747	9540	2328	3407	1510	307	233	185	3
Lognormal_2P	31	471	636	745	940	1430	941	5457	2088	3898	868	3111	48	15
Lognormal_3P	76	644	695	885	1474	604	417	1605	4993	729	3212	1139	4098	72	33
Loglogistic_3P	3	45	339	559	599	678	865	888	1213	6488	3968	2149	2850	24	8
Loglogistic_2P	4	22	42	98	268	291	460	907	733	5193	8765	2237	1657	2
Exponential_1P	68	217	456	459	465	750	535	3310	1726	512	538	7620	3895	56	71	1
Exponential_2P	144	332	684	694	742	355	449	1678	3164	462	510	3820	7628	17
Normal_2P	4	6	18	13	14	11	13	24	22	29	32	51	94	20347	1
Gumbel_2P	2	8	8	3	2	3	5	10	11	5	9	14	27	105	20466	1
Beta_2P		1		1		1	1		1		1

Outra importante observação é que a distribuição Normal é uma das piores funções a ser utilizada, o que comprova que o uso da Média em substituição a Mediana ou Moda não é possível.

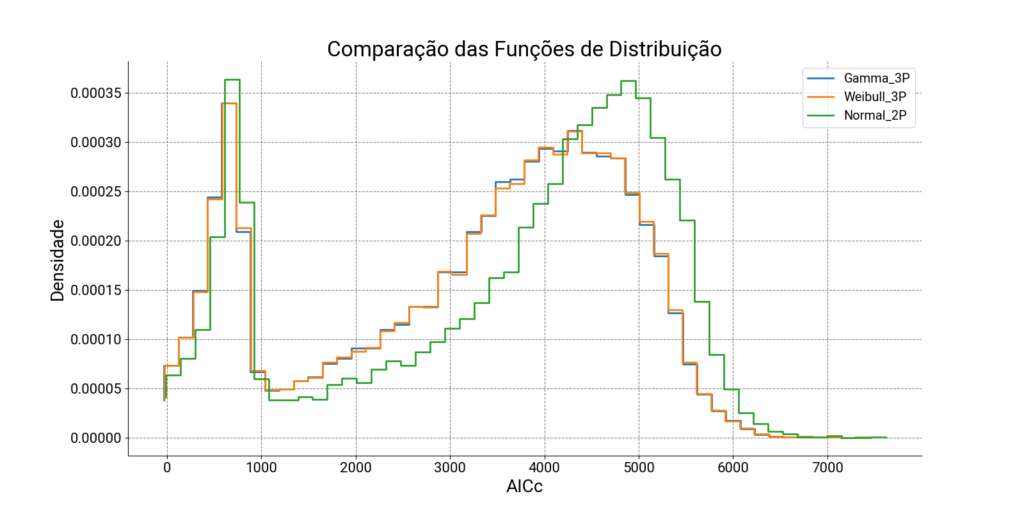
Menores AICc resultam uma melhor função de distribuição, portanto quanto maior a densidade em baixos valores de AICc melhor, ou seja, quanto maior a área sob a curva à esquerda melhor. A Figura 2 compara a distribuição do AICc entre as funções Gamma_3P, Weibull_3P e Normal_2P, mostrando a inferioridade da Normal.

As duas melhores funções são baseadas em composições de funções Weibull. A Gamma_3P e a Weibull_3P são as melhores opções de funções tradicionais e praticamente não há grande diferença entre elas, tendo ambas apresentado bons resultados. Existem mais referências bibliográficas de uso da Weibull em análise de confiabilidade e sobrevivência devido à sua versatilidade e interpretação intuitiva em termos de taxa de falha variável, por isso seu uso pode ser mais adequado.

A Figura 3 apresenta uma Weibull_3P ajustada aos dados da Figura 1.

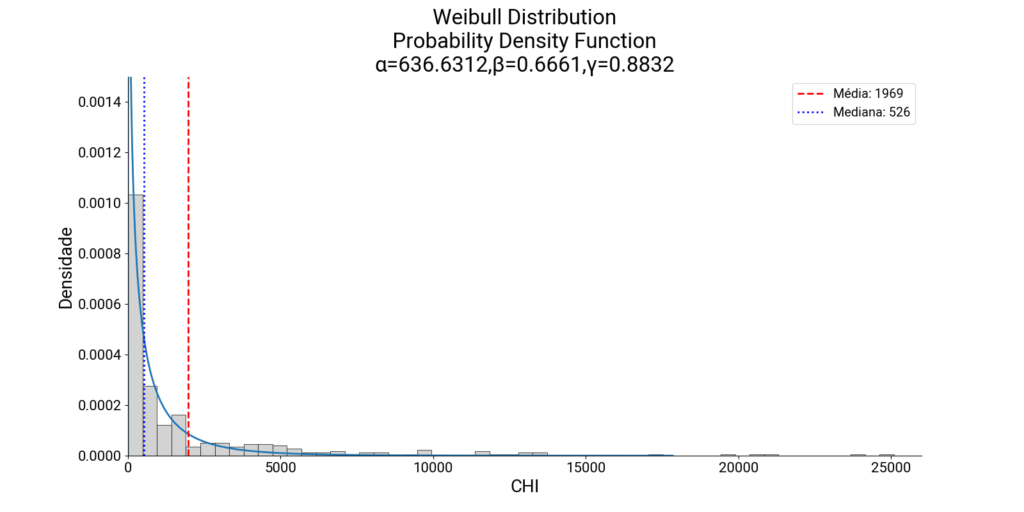
De posse da curva é possível qual estimar qual é a probabilidade de um dia com, por exemplo 25.000 CHI ocorrer novamente, sendo útil para análise de risco e melhoria no processo.

Os dados de parâmetros de todas as funções para cada conjunto elétrico, agente e ano está disponível em https://github.com/turkievicz/energianalytics/blob/main/notebooks/output/df_func_pars_full.parquet

Conclusões

Foi apresentada a diferença entre o uso da média e da mediana, com a última sendo mais adequada para interrupções de energia elétrica. O processo envolveu o teste de 16 funções de distribuição com a verificação dos valores de AICc, classificando as melhores distribuições para este uso específico. A Weibull_3P é sugerida como distribuição adequada, sendo simples, bem referenciada e de fácil ajuste.

Os dados apresentados aqui são fundamentados nos dados públicos disponíveis no site da ANEEL⁵ e o notebook que fundamentou esse estudo está disponível em https://github.com/turkievicz/energianalytics/blob/main/notebooks/analisa_melhores_funcoes_intrp.ipynb

Referências

1. DEC, FEC, CHI são conceitos de métricas definadas pela ANEEL no módulo 1 do PRODIST² ↩︎
2. Dia Crítico possui sua definição no item 2.129 do Módulo 1 do Prodist disponível em https://www2.aneel.gov.br/cedoc/aren2018842_prodist_modulo_1_v10.pdf ↩︎
3. A formulação de Tukey é amplamente utilizada em boxplot e o limite para definição de outlier baseia-se em +-1.5 o valor do interquartil. https://en.wikipedia.org/wiki/Outlier ↩︎
4. https://en.wikipedia.org/wiki/Akaike_information_criterion#AICc ↩︎
5. https://dadosabertos.aneel.gov.br/dataset/ccb25653-f07b-4f28-84c2-62a89d1f5a56 ↩︎